1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
module Helpers = 
  let permutations ls = 
    let rec insertions x = function
      | []             -> [[x]]
      | (y :: ys) as l -> (x::l)::(List.map (fun x -> y::x) (insertions x ys))
    let rec permutations' = function
      | []      -> seq [ [] ]
      | x :: xs -> Seq.concat (Seq.map (insertions x) (permutations' xs))
    ls |> permutations'
    
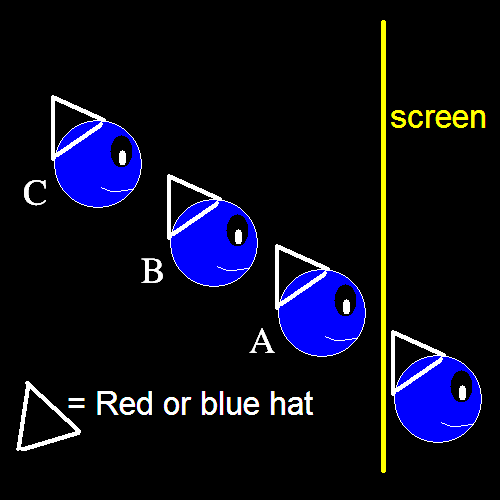
module PrisonersHatsPuzzle =
  type Hat = Red | Blue
  type Prisoner = Hat
  type Prisoners = Prisoner * Prisoner * Prisoner * Prisoner
  type Guess = Prisoners -> Prisoner * Hat

  // Bullet-proof logic for the prisoners to always go free:
  // 
  // As the fourth prisoner is behind a screen, we don't care about him.
  // If the last prisoner sees two equal colored hats, he knows he has the
  // the opposite and hereby he can call out the color.
  // In case the last prisoner doesn't call out his color, the second from
  // behind will know that he doesn't have the same color hat as the prisoner
  // in front of him, else the last one would have called it, hereby, he
  // can safely call out the opposite color of the prisoners hat in 
  // front of him.
  // 
  let guess : Guess =
    fun prisoners ->
      let a,b,c,d = prisoners
      match a,b,c,d with
        | (_,Red,Red,_)   -> a,Blue
        | (_,Blue,Blue,_) -> a,Red
        | (_,_,Blue,_)    -> b,Red
        | (_,_,Red,_)     -> b,Blue

open Helpers
open PrisonersHatsPuzzle

let hats = [Hat.Red; Hat.Blue; Hat.Red; Hat.Blue;]

let alwaysGoFree =
  permutations hats
  |> Seq.map(fun xs ->
    match xs with
      | a::b::c::d::[] -> a,b,c,d
      | _ -> failwith "never")
  |> Seq.map(fun x -> guess x)
  |> Seq.toArray

module Helpers = begin
  val permutations : ls:'a list -> seq<'a list>
end
module PrisonersHatsPuzzle = begin
  type Hat =
    | Red
    | Blue
  type Prisoner = Hat
  type Prisoners = Prisoner * Prisoner * Prisoner * Prisoner
  type Guess = Prisoners -> Prisoner * Hat
  val guess : Prisoner * Prisoner * Prisoner * Prisoner -> Prisoner * Hat
end

val hats : Hat list = [Red; Blue; Red; Blue]

val alwaysGoFree : (Prisoner * Hat) [] =
  [|(Blue, Blue); (Blue, Blue); (Blue, Blue); (Red, Red); (Red, Red);
    (Red, Red); (Blue, Blue); (Red, Red); (Red, Red); (Red, Red); (Blue, Blue);
    (Red, Red); (Red, Red); (Red, Red); (Blue, Blue); (Blue, Blue); (Red, Red);
    (Red, Red); (Blue, Blue); (Blue, Blue); (Blue, Blue); (Blue, Blue);
    (Blue, Blue); (Red, Red)|]